Sudoko, ludo per cifertabelo, klarigoj kaj sudokprogramo

Sudoko

Aŭtoro : Christian Bertin

Dato : 15-a de Januaro 2006

Elŝutebla programo, kiun mi faris, por generi kaj solvi sudokojn: sudokilo

1. Glosaro

Sudoko: tabelo el 9 linioj kaj 9 kolumnoj, dividita en  9 9-fakaj kvadratoj. En ĉiu linio, en ĉiu kolumno kaj en ĉiu 9-faka kvadrato, povas esti nur unu el la ciferoj 1 ĝis 9. Sudoki: ludi per sudoko, solvi sudokenigmon. Sudokisto: adepto de tiu sudokenigmo. Sudokanto: iu kiu sudokas. Subtabelo: ĉiu el la 9-fakaj kvadratoj, kiuj konsistigas sudokon.

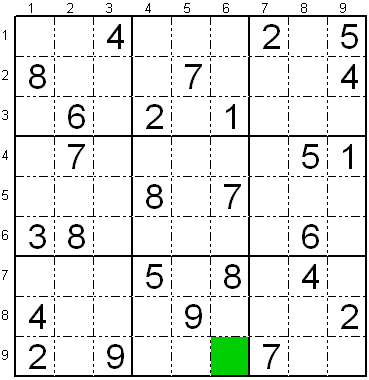
Jen komenca sudoko. Komence la sudoko enhavas nur proksimume unu trionon da fakoj kun ciferojn kaj la aliaj fakoj estas liberaj, kiel montras la apuda bildo. Normala sudoko havas nur unu solvon, sed povas esti sudokoj, kiuj havas plurajn solvojn. Solvi sudokon signifas meti ciferojn en ĉiujn liberajn lokoj tiel ke cifero estu nur unu-foja en ĉiu linio, en ĉiu kolumno kaj en ĉiu 9-faka subtabelo, kie ĝis estas.

Jen kelkaj reguloj, komencante per la plej simpla.

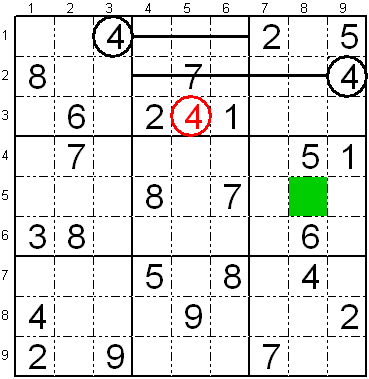
Unua regulo (deviga cifero pro du jam metitaj ciferoj) Por ĉiu cifero, kiu aperas dufoje en tri sinsekvaj korizontalaj subtabeloj, kontrolu ĉu en la subtabelo, kie mankas tiu cifero, estas nur unu libera fako sur la tria linio. En tiu kazo metu tiun ciferon. Same faru por la du alia sinsekvaj vicoj de 3 subtabeloj. Same faru laŭ la kolumnoj por ĉiu kolumno de 3 sinsekvaj subtabeloj. Sur la apuda sudoko, laŭ la unua regulo, vi devus sukcesi meti la ciferon: "2" sur la verda fako sur la tria subtabelo de la dua vico de subtabeloj L5K8, "4" sur la unua subtabelo de la dua vico de subtabeloj L5K2, "8" sur la tria subtabelo de la dua vico de subtabeloj L4K7, "8" sur la dua subtabelo de la unua vico de subtabeloj L1K5, "2" sur la dua subtabelo de la tria vico de subtabeloj L7K5 Vi povas vidi la rezulton sur la bildo por klarigi la duan regulon.

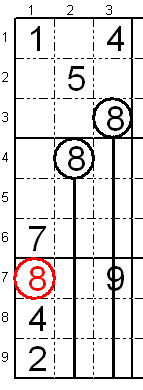
Dua regulo (deviga cifero pro tri jam metitaj ciferoj) Vi jam provis la unua regulon kun la cifero "8" en la unua kolumno de 3 subtabeloj sed bedaŭrinde estas du liberaj fakoj sen tiu cifero sur la tria kolumno, kiu trairas la 3 subtabelojn. Tiam vi devas kontroli ĉu la sama cifero ne estas jam sur unu el la linioj, kiuj trairas tiujn liberajn fakojn. Se tiu cifero estas sur linio el tiuj liberaj fakoj, tiam restas nur unu fako por meti la ciferon. Same faru por la tri sinsekvaj vicoj de 3 subtabeloj. Same faru laŭ la kolumnoj por ĉiu kolumno de 3 sinsekvaj subtabeloj. 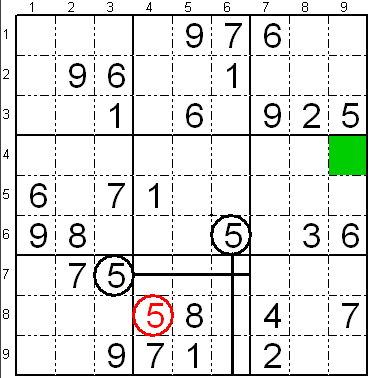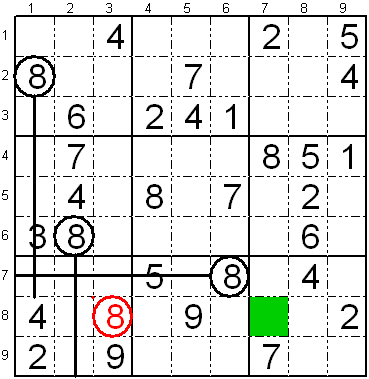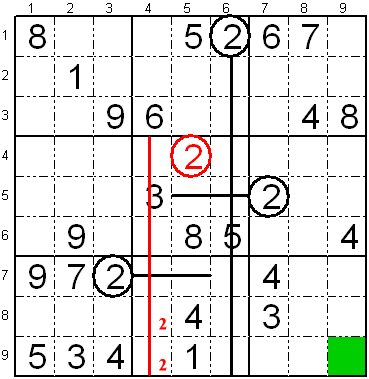Sur la apuda sudoko, laŭ la nuna aŭ la unua regulo (kun la novaj ciferoj), vi devus sukcesi meti la ciferon "7" sur la dua subtabelo de la lasta vico de subtabeloj L8K4, "5" sur la tria subtabelo de la lasta vico de subtabeloj, kie estas verda fako, "4" sur la tria subtabelo de la dua vico de subtabeloj L6K7, "7" sur la tria subtabelo de la dua vico de subtabeloj L6K9, "5" sur la unua subtabelo de la tria vico de subtabeloj L9K2, "5" sur la dua subtabelo de la unua vico de subtabeloj L2K6, "6" sur la lasta subtabelo de la unua vico de subtabeloj L2K7,

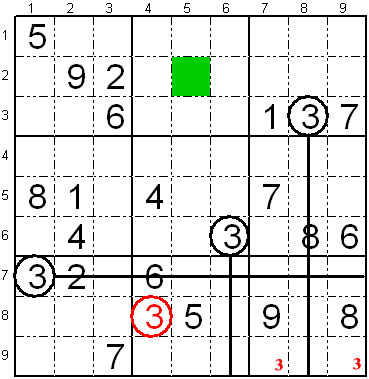
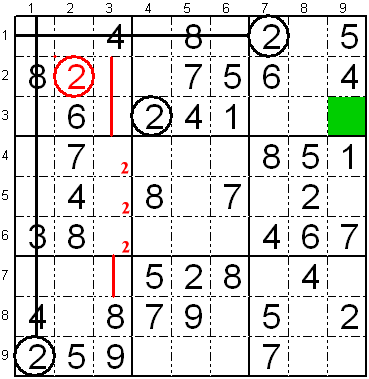
Tria regulo (deviga cifero pro ne jam metita deviga sama cifero) Rigardu la apudan sudokon. Laŭ la unua regulo restas du fakoj, kie eblas meti ciferon "2", tio estas sur la dua kaj tria fakoj de la dua linio de la unua subtabelo (L2K2 kaj L2K3). Sed rigardu la unuan subtabelon de la dua vico de subtabeloj. En tiu subtabelo, la dua kolumno estas kompleta. Sekve la cifero "2", kiu jam estas sur la unua kolumno de la sudoko, povas esti nur sur la tria kolumno de tiu subtabelo. Pro tio, sur la unua subtabelo de la sudoko, la cifero ne povas esti en la tria kolumno, kaj do restas unu fako por la cifero "2" la fako L2K2 (Dua linio, dua kolumno). Vi jam provis la unua regulon kun la cifero "8" en la unua kolumno de 3 subtabeloj sed bedaŭrinde estas du liberaj fakoj sen tiu cifero sur la tria kolumno, kiu trairas la 3 subtabelojn.

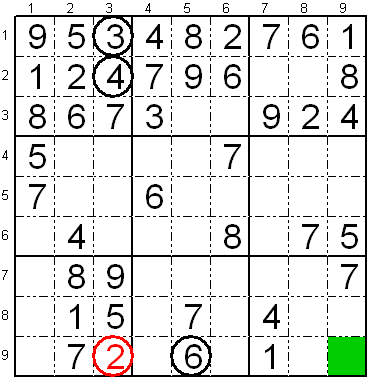
Kvara regulo (deviga cifero pro ne metebleco de la aliaj mankaj ciferoj) Rigardu la apudan sudokon. Sur la unua subtabelo de la lasta linio de subtabeloj, mankas la ciferoj "2", "3", "4" kaj "6". Se vi rigardas al la fako L9K3 (9-a linio kaj 3-a kolumno), la ciferoj "3", "4" kaj "6" estas jam sur la kolumno aŭ sur la linio, kiu trairas tiun fakon, sekve nur la cifero "2" estas metebla sur tiu fako.

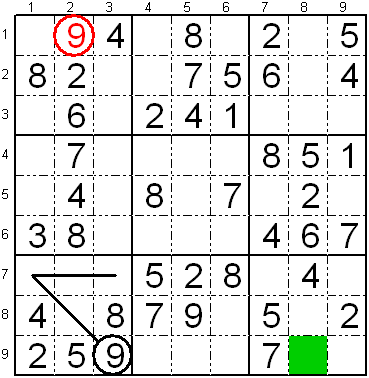
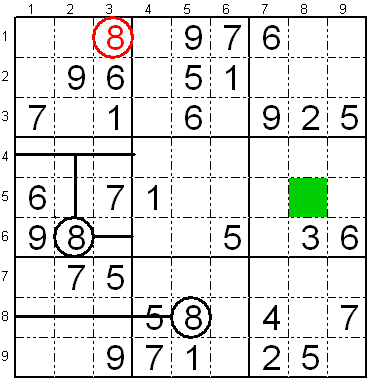
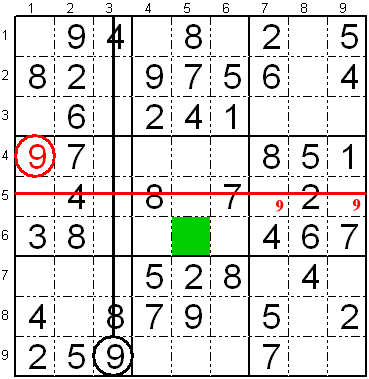
Kvina regulo (deviga cifero pro neebleco meti ĝin aliloke sur la sama linio aŭ kolumno) Rigardu la apudan sudokon. En la dua kolumno, mankas la ciferoj "1", "3" kaj "9". Estas tri liberaj fakoj, unu L1K2 sur la unua subtabelo de la unua vico de subtabeloj kaj la du aliaj L7K2, L8K2 en la unua subtabelo de la tria vico de subtabeloj. La cifero "9" estas jam en la unua subtabelo de la tria vico de subtabeloj, sekve ĝi ne estas metebla sur la aliaj fakoj de la sama subtabelo, do restas unu fako por ĝi: L1K2

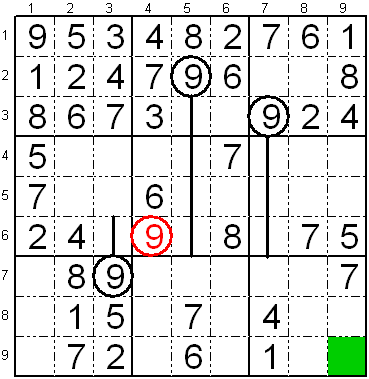
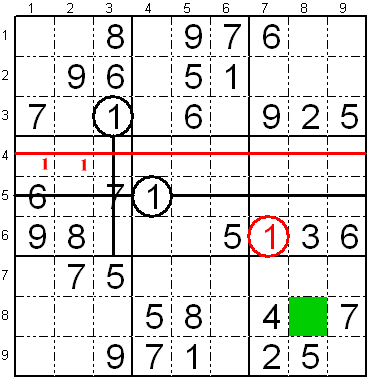
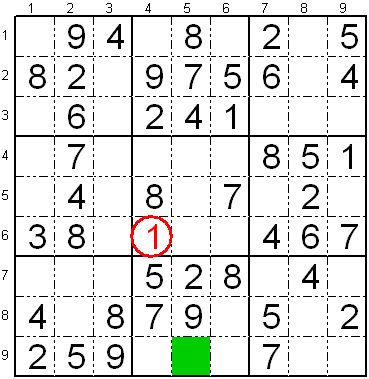
Sesa regulo (deviga cifero  pro esto de ĉiuj aliaj ciferoj sur la linio, kolumno aŭ subtabelo de tiu libera fako) Rigardu la apudan sudokon. Cifero estas metebla sur libera fako, se ĝi ne jam estas aliloke sur la kolumno aŭ la sur la linio, kiuj trairas ĝin. En la 4-a kolumno estas la ciferoj    "-2--5-789"   kaj en la 6-a linio estas la ciferoj    "--34-678-". Se oni aldonas ilin, la kunigitaj ciferoj estas "-23456789". Vi tiel konstatas, ke mankas nur la cifero "1", do vi prave povas meti ĝin. Se post tiu kunmetiĝo de la ciferoj jam metitaj sur la kolumno kaj la linio restas pluraj meteblaj ciferoj, tiam vi povas forigi ankaŭ tiujn, kiu estas metitaj en la responda subtabelo de la libera fako, en nia kazo "------78-"

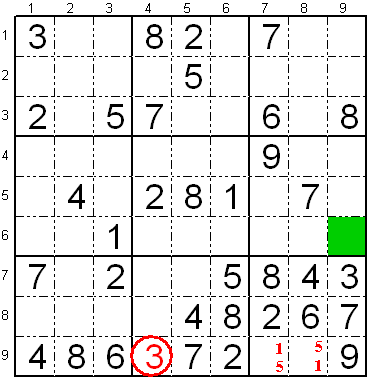
Sepa regulo (deviga cifero pro devigo meti la aliajn ciferojn aliloke) Rigardu la apudan sudokon. Sur la lasta linio, mankas la ciferoj "1", "3" kaj "5". Devige la ciferoj "1" kaj "5" devas esti sur la lasta subtabelo de la tria vico de subtabeloj, eĉ se oni ne povas diri ĉu estos "1" en L9K7 aŭ en L9K8. Sekve restas nur la cifero "3" por la libera fako de la dua subtabelo.